Item Durability - Discoveries

So back to item durability...

I simulated some more results, trying solutions 1. (increase the total resistance drastically) and 2. (set a breakpoint after which rolls can start).

Fun times!

Solution 1.

So solution 1 essentially just elongates an item's lasting time. This meant attempting to graph how the average lasting time in days changed as the total resistance grew. Here's a graph of those results with some best-fit functions.




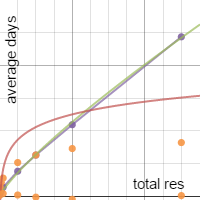
I found that the purple line (that's the actual data points - orange is resistance/days) was most closely represented as an exponential of the form y = m x^k. Desmos calculated m and k to both be fairly small: m = 0.024115 and k = 0.8247.

Armed with this knowledge, I can estimate how long items will last with a given total resistance. Some resistances which were too big to calculate should be about:

1,000,000 total resistance: 2,145 days (5.86 years)
2,000,000 total resistance: 3,790 days (10.39 years)
5,000,000 total resistance: 8,071 days (22.11 years)

The kind of equipment with such enormous total resistance would need to be very well-crafted, but consider how long some of our medieval discoveries have lasted; many still sit in museums today, centuries later. which would need an enormous total resistance (over 20,000,000 if 5,000,000 gives us 22 years). Of course, what percent of the whole are they? A very small well-protected group?

Unfortunately, my best-fit function is only a best-fit function. Were I to add more data points it would presumably get a bit closer to the actual values, but again my actual values are based on 2,000 random number generations so who knows how accurate they actually are.

Solution 2.

For the breakpoint in solution 2, I was running out of processing power so I ran two tests on 10,000 resistance: one with 2,000 items, a breakpoint of 300 and a roll of 1d8, another on 500 items, a breakpoint of 2,000 and a roll of 1d20. So that was a bad move because I wasn't controlling my variables properly. Anyway...

The results were very close to the breakpoint divided by the average die roll, which made sense to me. The first test had an average number of days of 93.94, an extra three weeks or so over the 10,000 resistance test with no breakpoint. The second test had an average number of days of 194.41, so six months more or so. Note that 300/4.5 = 66.6 (first test) and 2000/10.5 = 190.48 (second test). These numbers estimate the approximate point in days at which the breakpoint is reached based on the average die roll, and the larger that number the closer it ends up being to the average (as the item breaks sooner when the breakpoint corresponds to a higher percentage).

Based on this information, we can estimate the lasting time of items with other breakpoints:
1,000 breakpoint, 1d8 roll: 222.22 days.
2,000 breakpoint, 1d8 roll: 444.44 days.

5,000 breakpoint, 1d4 roll: 2,000 days.

As we can see, adding breakpoints essentially gives us a linear progression, which was what I was trying to avoid by using an exponential distribution. So let's can the breakpoint idea.

Back to Solution 1.

While running these tests, I considered some more information. For many of these simulations, the average break chance tended to be quite low when the item broke, and was becoming smaller and smaller. However, once the break chance becomes less than 1%, the roll will never be small enough to break the item (can't roll 0 unless we change our d100 rules, which would probably enrage my players). Let's calculate the stress level needed to reach 1% for a few large resistance values.

This is in fact also a linear progression:

F(x) = 1 - exp(-x/k) (k is the total resistance, x is the number of days passed)
0.01 = 1 - exp(-x/k)
exp(-x/k) = 0.99
-x/k = ln(0.99)
x = -ln(0.99)*k
(-ln(0.99) ~= 0.01)

As we modify k, x becomes larger (it appears linear but is actually a negative natural logarithmic progression as the function suggests).

500,000 total resistance: 5,000 days
1,000,000 total resistance: 10,000 days
etc. (1% is reached at 1% of the total resistance)

Well that wasn't very exciting. This pattern continues along the trend of ln(z) for larger minimum break chance values z, but gradually differs along the negative natural logarithm:

F(x) = 0.06 --> x = -ln(0.94)*k ~= 0.062*k
F(x) = 0.1 --> x = -ln(0.9)*k ~= 0.105*k
F(x) = 0.25 --> x = -ln(0.75)*k ~= 0.288*k

If we graph THIS part...

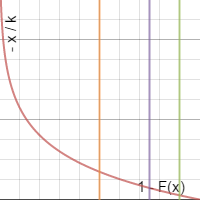
This data essentially replicates our old cumulative distribution but it's inverted, emphasizing that a smaller break chance also corresponds to the stress taken being farther from the mean.

Well duh.

So no matter what method I use, since at very large numbers the item tends to break around 1%, I can simply increase the number by some linear amount (multiple all the total resistances up) to get my desired rates.

But something about that still bugs me. It doesn't seem like it would be very fun for the player: you track the number of days for years and years of play, never having to roll until finally the odds are 1% and you need to start rolling. Then you play for a long time longer until your d100 comes up 1 and your item breaks. Essentially there's still a break point being forced by the fact that the d100 can only represent up to 2 decimal places of the percent chance.

This is bothersome, but also tells me something about how die-rolling works, I suppose. If I were to use smaller dice (like a d20), the players would simply lose their items later (once the chance reaches 5%). Using a system to obtain larger numbers than 100, like a d1000, seems too annoying to make the players do and would of course make their items disappear sooner, which would then require larger total resistances.

Musings.

When I had set out to accomplish an effective item durability generator, I wanted to make equipment an important weight on the minds of the players, by adding the tension of "Will my gear survive this adventure?" While it can be very frustrating to have no usable weapons, the advantage of D&D's freeform design is that players can make weapons out of anything and find weapons anywhere, as long as they have the necessary tools. They don't need to be stuck weaponless for ages as some kind of purgatory punishment for not packing well, and they'll remember for next time. I don't want to condemn them to endless suffering.

So I imagined my players having to examine their equipment before going out. If they were going off into the wilderness, they would need to pack some tools to repair and care for their gear, or extra parts to replace what did break. There's always the risk in a fight that your weapon breaks, or you slip on the trail and the bottom of your pack gets torn open, or the clumsy cleric shatters the statuette when he pulls it off the pedestal and the floor quakes. These are all circumstances where equipment durability can matter.

A satisfying solution should have a small chance of breakage which gradually grows, starting at a small enough chance that the player would never expect the equipment to break, and gradually increasing as the equipment is worn and used. If a player doesn't make an effort to take care of the item, it risks falling apart.

There is another way to represent numbers smaller than 0.01 without using enormous dice, of course. Use multiple successive rolls. If the first d20 turns up as a 1, roll again to see if you get closer to breaking your equipment. Two successive 1s is already 0.0025: a quarter of the frequency of a 1 on a d100.

Realistically, if you have a 5% chance of breaking something every day you heft it around, it should break pretty soon. So to keep things exciting I'd probably want the break chance to stay below 10%. That way, if the item was simply left alone after that, it should survive nicely (if the stress increases by 1 every turn, an item with total resistance 10,000 lasts 181.38 days on average; around 2.6 times as long as when it increases by 1d8 every turn).

Extraordinary circumstances should certainly risk destroying items, but fundamentally I want players to have items that have survived everything which the players can cherish: the magical bow that has lasted through a dragon's breath or the hammer that fell 300 feet and was still usable.

Equipment certainly needs a counter which controls how close it is to breaking: falls and spells and all those goodies will drive that number up, but otherwise the equipment should make it through the day safely.

Given these requirements, I'm thinking the best way to fix up the generator is to add more conditionals: certain situations apply stress and others don't. What counts for more? There's already a total amount of stress an item can take, so there's no need to have all these different rolls based on material (unless I made all the totals the same and just modified the tolerance). The different rolls can instead correspond to stress type.

Then an item's survival becomes less certain: your gear should make it through the mountains, but what if something goes wrong?

Furthermore, there should be a way to repair and improve the durability of gear. I'm going to look over the mending spell and consider some options in that respect.

Lastly, the system shouldn't be too obtrusive: I don't want the players having to roll the survival of every piece at the end of every day themselves. That's simply too annoying. So whatever solution I settle on should be implementable as an app or Excel table.

Well, we aren't out yet!

The Dungeon's Front Door Review

Recently, Alexis Smolensk over at the Tao of D&D published his second collection of essays, The Dungeon's Front Door & Other Things in the Deep Dark. Much like the first collection, How to Play a Character, DFD is a small but dense volume of essays that investigate a wide variety of topics. While How to Play was a compilation of various excellent posts from Alexis' blog, however, DFD takes the theme of dungeons and injects it throughout.

The result is a cheerful romp through the notion of dungeons in D&D. Alexis has changed his format slightly for this collection. Interspersed among the thirteen essays in the book are two short stories and one series of examples. I was pleasantly surprised to discover these: on his blog, Alexis tends to offer a lot of critical analysis but does not necessarily delve into the specifics of his method, a mystery which encourages the reader to devise their own solution and then toy with the implementations.

There are a few central tenets which are put forward. One is the importance of dungeons themselves. Alexis totes the dungeon as a world within a world, a place where the players can retreat from the chaos of the enormous outdoors into a confined, orderly box. To do so effectively, Alexis emphasizes the value of making the dungeon a world. What is possibly the best essay in the book (it's certainly my favourite), "Wyrd," chronicles the history for a mountain cave that is home to both a goblin community and some hungry jellies. "Wyrd" emphasizes the importance of having a closed system to your dungeons: where does food come from? where do tools come from? what are the defenses of the dungeons' inhabitants? Certain oddities, like untouched doors or piles of treasure, may seemingly defy the sense of the outside world, but Alexis reminds the reader that the dungeon is not like the outside world. It's alien and strange, and so are its people many a time. Maybe they revere doors? Maybe there's an old fountain deep down below which spits out coins? Who knows?

The DM might have some ideas. But the players may never know. Alexis again highlights the value of keeping one's hand close to one's chest while DMing. In "Wyrd," the players may arrive at any point during the history of the dungeon, and find something entirely different waiting for them. They may never know what happened. But a DM with such knowledge can cultivate a little mystery and a little strangeness to keep the players' emotions running high. Alexis recommends a little toying with the players' emotions to do so: his essay "Breaking the Fourth Wall" is all about playing with the players' fears. Little pranks when done right can provide a lot of extra fuel for keeping the players amped and excited, much like a rollercoaster ride.

And there should be lots of strangeness and mystery! DFD rightfully points out that real estate is expensive when you're carving through stone. This is an excellent point: though the dungeon is its own world, it's a small world. One door may be all that stands between the orcs and the gnolls. A pit may service both a hungry otyugh and goblins with garbage. Making your dungeons small, DFD explains, allows for every room to have a purpose (which the players may not understand). And often that purpose is fear. The dungeon is not something to be made gentle or welcoming, but a struggle to victory. This is one of the most important points of the essay, and in my opinion one of the best: the more the players fight, the sweeter victory is. The DM is on the players' side to help them accomplish this high, and DFD explains that by using busy dungeons and a gentle dose of evil, players can be given quite the incredible ride.

This is the majority of DFD, but the short "story" essays "Rest" and "Dungeon Extractions, Inc." are not merely diversions from Alexis' critical analyses. "Rest" features an account of a party trapped in a massive dungeon -- some of its references (the dwarf is the first to become upset by the fact that the party has been in the dungeon for "six hundred and twenty-two" days) are later explored in Alexis' essay on megadungeons "A Door Too Far." The story is humorous and showcases some of the absurdities of the dungeon, especially its attractive power. Even after such an enormous amount of time, by which point decisions like which fork to take become tedious, or after treasure, left behind (cannot be carried), has lost all real value, the party slogs forward.

"Dungeon Extractions, Inc." presents the success of a man who has essentially "industrialized" the dungeon crawl. A billionaire entrepreneur, Sir Phelonious (sounds like felonious, no?) the Elf has min-maxed a massive extraction team to capitalize on dungeons across the world, raking in billions in profits. Of course, Phil is aware that his business will soon cause economic collapse and the whole industry will fall apart: Alexis' characters are charmingly genre-savvy (as many D&D players are).

"Flora in the Recesses" is another fun diversion in the book, relatively sparse on Alexis' usual argumentation. Instead, Alexis puts his methods into action to display how the dungeon is justified, inventing plants to inhabit dungeons and to feed their residents. The plants integrate smoothly with the design of dungeon monsters: intensely peculiar but detailed enough to seem natural. It's a wonderful example of dungeon-world design.

All in all, The Dungeon's Front Door is a great read for DMs in need of a kickstart to reinvigorating their dungeons. It's unfortunately a short read, but nonetheless a valuable one on the philosophy of the dungeon. I am excited to experiment with its suggestions for my players.

The book is currently 20% off on Amazon, and you can also purchase it on Lulu.

Thoughts on the Item Durability Generator

I've been working on the item durability generator for a while now, mainly to get a working Android version up. I've gotten the preliminaries done and had some time to analyze how the generator is working.

One main problem has crept up once I started using the generator, however: items are breaking too soon.

When I developed the idea, the total resistance of an item was supposed to be its average durability in days: how long it should last on average before breaking. I was finding that items with a durability of 500 days were lasting for 6; items with a durability of 200,000 days were lasting for 500. So I investigated the cause.

What I found was that random variables were, as they often are, the cause. Each time the stress is added, there is also a d100 roll to see if the item breaks. Obviously, given the uniform distribution of die rolls, after about 100 of them (and much before too) I had a good chance of getting below the break chance.

I tested this on a bunch of different simulations: 2000 items of various total resistances. My findings were as follows:

Resistance: 500
Average # of Days Lasted: 13.06
Standard Deviation # of Days Lasted: 6.87
Average Break Chance when Item Broke: 12%
Standard Deviation of Break Chance when Item Broke: 5.33%

Resistance: 2,000
Average # of Days Lasted: 27.84
Standard Deviation # of Days Lasted: 14.03
Average Break Chance when Item Broke: 6%
Standard Deviation of Break Chance when Item Broke: 2.91%

Resistance: 5,000
Average # of Days Lasted: 46.22
Standard Deviation # of Days Lasted: 21.84
Average Break Chance when Item Broke: 4%
Standard Deviation of Break Chance when Item Broke: 1.87%

Resistance: 10,000
Average # of Days Lasted: 70.58
Standard Deviation # of Days Lasted: 31.11
Average Break Chance when Item Broke: 3%
Standard Deviation of Break Chance when Item Broke: 1.34%

Resistance: 50,000
Average # of Days Lasted: 192.79
Standard Deviation # of Days Lasted: 62.91
Average Break Chance when Item Broke: 2%
Standard Deviation of Break Chance when Item Broke: 0.55%

Resistance: 200,000
Average # of Days Lasted: 547.05
Standard Deviation # of Days Lasted: 99.83
Average Break Chance when Item Broke: 1%
Standard Deviation of Break Chance when Item Broke: 0.21%

As you can see, the number of days increases while the break chance decreases. I've been contemplating a few solutions to this problem which I will outline in a future post, but they are as follows:

1. Increase all items' resistance to very large values in order to get an average closer to what I expected.
2. Only begin rolling break chance after a certain point.
3. Reconfigure the system.

Time to weigh options!

Item Durability

So back in November I read about a fun idea on the Tao of D&D, discussing item breakage. In my mind, D&D could certainly use a little more caution and preparation, as if the players put in lots of time and effort to be equipped to achieve their goals, their goals will feel sweeter once they are achieved. So to insert a bit of tension and fun/stress (a little stress is exciting after all), I developed a program as Alexis suggests in the linked post.

It's an Excel file which requires macros and VBA and such, along with iterative manual calculations. Also, it's generally very ill-advised to download Excel files off the Internet which have built-in macros as there are a whole host of security issues you risk exposing yourself to. So if you don't feel comfortable then don't download it.

Here's the basic appearance of the generator:

It works very simply. You first tell it whether you want to generate a new item or not. The generator then, using the specified material and quality of the item, along with whether or not the item is magical, generates a number which corresponds to the total "resistance" in days of that item, along with helpfully informing you of the item's stress tolerance.

Once the total resistance has been generated, you tell the sheet not to generate a new item any more and recalculate.

As you can see, the generator has produced a number of "Stress Taken," again in terms of days. This represents how, over the course of one day of use, the item has fared. It is understood that, were the item to be placed in a vault constantly and regularly cleaned and maintained, the stress taken would be 1. The number instead generated represents the stress of regular use on the item, which is hence larger.

The "Break Chance" beside "Stress Taken" shows the chance the item will now break on a d100. It is calculated using a cumulative exponential distribution function where x is the stress taken and lambda is the inverse total resistance. This function means that the item's break chance should be around 66% once it reaches its total resistance, so the item can actually survive past the total resistance date. The reason "Break Chance" exists is that sometimes, though the item shouldn't break for a long time, it does anyway, perhaps due to a fracture in the material or a freak accident. Maybe the character is just really clumsy.

Right now, that chance is 0%, so there's no need to roll. But let's say that the next day comes around, and the character carrying this poor iron item - say an old dagger - also falls off a parapet forty feet above the ground. Now the character takes fall damage, and so does the item.

The character took 15 damage from the fall, which was also added to the item (the item also took another 5 stress damage during the day, bringing us up to 23). As the total resistance is quite high, there still is no chance of breaking.

Let's say the character then enters a dungeon, falls into a 20-foot pit and spends 3 days fighting troglodytes to get back to the entrance. Here's how the dagger has held up:

It has now taken 47 stress and has a break chance of 2%, so at the end of the day, the character will also need to roll a d100 to see if the item breaks. 

100 days pass and the item takes a bit more of a beating:

Now it has a 22% chance to break! Yikes! It's only made it 105 days from when the character first received it.

Anyways, that concludes a brief intro of the generator. Here is a link for those interested in using it. I will try posting a more detailed version of it later, which also includes a basic character sheet.

https://drive.google.com/file/d/0Bw6d7rcFKzN4b0x4U3RCWFhfYTA/view?usp=sharing

I may make a few edits to the file as time goes on.

Reinventing the Wheel

Well I quickly lost my steam on that last topic. My world tends to be in a pretty regular flux, and my players don't play often enough for me to get comfy sitting still on it.

Instead, I decided to reinvent the Wheel. The shape bugged me and it did not feel medieval enough, so for the next little while I will be working on adding all that content back onto this:

I think that looks a lot more like a wheel, no? (I did put an overlay on top to keep that part clear!)

I worry of course that I will change it again. Given the length of time between games, I may end up putting off a world map for a while and focussing on creating small, modular areas which could be later incorporated into an entire world.