Item Durability - Discoveries

So back to item durability...

I simulated some more results, trying solutions 1. (increase the total resistance drastically) and 2. (set a breakpoint after which rolls can start).

Fun times!

Solution 1.

So solution 1 essentially just elongates an item's lasting time. This meant attempting to graph how the average lasting time in days changed as the total resistance grew. Here's a graph of those results with some best-fit functions.




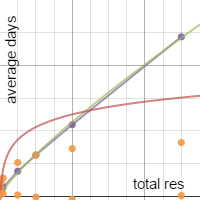
I found that the purple line (that's the actual data points - orange is resistance/days) was most closely represented as an exponential of the form y = m x^k. Desmos calculated m and k to both be fairly small: m = 0.024115 and k = 0.8247.

Armed with this knowledge, I can estimate how long items will last with a given total resistance. Some resistances which were too big to calculate should be about:

1,000,000 total resistance: 2,145 days (5.86 years)
2,000,000 total resistance: 3,790 days (10.39 years)
5,000,000 total resistance: 8,071 days (22.11 years)

The kind of equipment with such enormous total resistance would need to be very well-crafted, but consider how long some of our medieval discoveries have lasted; many still sit in museums today, centuries later. which would need an enormous total resistance (over 20,000,000 if 5,000,000 gives us 22 years). Of course, what percent of the whole are they? A very small well-protected group?

Unfortunately, my best-fit function is only a best-fit function. Were I to add more data points it would presumably get a bit closer to the actual values, but again my actual values are based on 2,000 random number generations so who knows how accurate they actually are.

Solution 2.

For the breakpoint in solution 2, I was running out of processing power so I ran two tests on 10,000 resistance: one with 2,000 items, a breakpoint of 300 and a roll of 1d8, another on 500 items, a breakpoint of 2,000 and a roll of 1d20. So that was a bad move because I wasn't controlling my variables properly. Anyway...

The results were very close to the breakpoint divided by the average die roll, which made sense to me. The first test had an average number of days of 93.94, an extra three weeks or so over the 10,000 resistance test with no breakpoint. The second test had an average number of days of 194.41, so six months more or so. Note that 300/4.5 = 66.6 (first test) and 2000/10.5 = 190.48 (second test). These numbers estimate the approximate point in days at which the breakpoint is reached based on the average die roll, and the larger that number the closer it ends up being to the average (as the item breaks sooner when the breakpoint corresponds to a higher percentage).

Based on this information, we can estimate the lasting time of items with other breakpoints:
1,000 breakpoint, 1d8 roll: 222.22 days.
2,000 breakpoint, 1d8 roll: 444.44 days.

5,000 breakpoint, 1d4 roll: 2,000 days.

As we can see, adding breakpoints essentially gives us a linear progression, which was what I was trying to avoid by using an exponential distribution. So let's can the breakpoint idea.

Back to Solution 1.

While running these tests, I considered some more information. For many of these simulations, the average break chance tended to be quite low when the item broke, and was becoming smaller and smaller. However, once the break chance becomes less than 1%, the roll will never be small enough to break the item (can't roll 0 unless we change our d100 rules, which would probably enrage my players). Let's calculate the stress level needed to reach 1% for a few large resistance values.

This is in fact also a linear progression:

F(x) = 1 - exp(-x/k) (k is the total resistance, x is the number of days passed)
0.01 = 1 - exp(-x/k)
exp(-x/k) = 0.99
-x/k = ln(0.99)
x = -ln(0.99)*k
(-ln(0.99) ~= 0.01)

As we modify k, x becomes larger (it appears linear but is actually a negative natural logarithmic progression as the function suggests).

500,000 total resistance: 5,000 days
1,000,000 total resistance: 10,000 days
etc. (1% is reached at 1% of the total resistance)

Well that wasn't very exciting. This pattern continues along the trend of ln(z) for larger minimum break chance values z, but gradually differs along the negative natural logarithm:

F(x) = 0.06 --> x = -ln(0.94)*k ~= 0.062*k
F(x) = 0.1 --> x = -ln(0.9)*k ~= 0.105*k
F(x) = 0.25 --> x = -ln(0.75)*k ~= 0.288*k

If we graph THIS part...

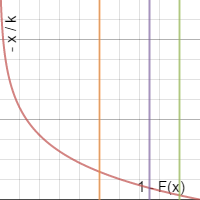
This data essentially replicates our old cumulative distribution but it's inverted, emphasizing that a smaller break chance also corresponds to the stress taken being farther from the mean.

Well duh.

So no matter what method I use, since at very large numbers the item tends to break around 1%, I can simply increase the number by some linear amount (multiple all the total resistances up) to get my desired rates.

But something about that still bugs me. It doesn't seem like it would be very fun for the player: you track the number of days for years and years of play, never having to roll until finally the odds are 1% and you need to start rolling. Then you play for a long time longer until your d100 comes up 1 and your item breaks. Essentially there's still a break point being forced by the fact that the d100 can only represent up to 2 decimal places of the percent chance.

This is bothersome, but also tells me something about how die-rolling works, I suppose. If I were to use smaller dice (like a d20), the players would simply lose their items later (once the chance reaches 5%). Using a system to obtain larger numbers than 100, like a d1000, seems too annoying to make the players do and would of course make their items disappear sooner, which would then require larger total resistances.

Musings.

When I had set out to accomplish an effective item durability generator, I wanted to make equipment an important weight on the minds of the players, by adding the tension of "Will my gear survive this adventure?" While it can be very frustrating to have no usable weapons, the advantage of D&D's freeform design is that players can make weapons out of anything and find weapons anywhere, as long as they have the necessary tools. They don't need to be stuck weaponless for ages as some kind of purgatory punishment for not packing well, and they'll remember for next time. I don't want to condemn them to endless suffering.

So I imagined my players having to examine their equipment before going out. If they were going off into the wilderness, they would need to pack some tools to repair and care for their gear, or extra parts to replace what did break. There's always the risk in a fight that your weapon breaks, or you slip on the trail and the bottom of your pack gets torn open, or the clumsy cleric shatters the statuette when he pulls it off the pedestal and the floor quakes. These are all circumstances where equipment durability can matter.

A satisfying solution should have a small chance of breakage which gradually grows, starting at a small enough chance that the player would never expect the equipment to break, and gradually increasing as the equipment is worn and used. If a player doesn't make an effort to take care of the item, it risks falling apart.

There is another way to represent numbers smaller than 0.01 without using enormous dice, of course. Use multiple successive rolls. If the first d20 turns up as a 1, roll again to see if you get closer to breaking your equipment. Two successive 1s is already 0.0025: a quarter of the frequency of a 1 on a d100.

Realistically, if you have a 5% chance of breaking something every day you heft it around, it should break pretty soon. So to keep things exciting I'd probably want the break chance to stay below 10%. That way, if the item was simply left alone after that, it should survive nicely (if the stress increases by 1 every turn, an item with total resistance 10,000 lasts 181.38 days on average; around 2.6 times as long as when it increases by 1d8 every turn).

Extraordinary circumstances should certainly risk destroying items, but fundamentally I want players to have items that have survived everything which the players can cherish: the magical bow that has lasted through a dragon's breath or the hammer that fell 300 feet and was still usable.

Equipment certainly needs a counter which controls how close it is to breaking: falls and spells and all those goodies will drive that number up, but otherwise the equipment should make it through the day safely.

Given these requirements, I'm thinking the best way to fix up the generator is to add more conditionals: certain situations apply stress and others don't. What counts for more? There's already a total amount of stress an item can take, so there's no need to have all these different rolls based on material (unless I made all the totals the same and just modified the tolerance). The different rolls can instead correspond to stress type.

Then an item's survival becomes less certain: your gear should make it through the mountains, but what if something goes wrong?

Furthermore, there should be a way to repair and improve the durability of gear. I'm going to look over the mending spell and consider some options in that respect.

Lastly, the system shouldn't be too obtrusive: I don't want the players having to roll the survival of every piece at the end of every day themselves. That's simply too annoying. So whatever solution I settle on should be implementable as an app or Excel table.

Well, we aren't out yet!